직육면체 부피와 겉넓이 사다리꼴 넓이 공식 알아보기 PDF 자료 다운로드
수학적인 지식은 우리의 일상 생활과 밀접하게 연관되어 있습니다. 특히, 직육면체와 같은 기본적인 도형의 부피와 겉넓이를 계산하는 것은 건축, 공학, 포장 디자인 등 다양한 분야에서 중요한 역할을 합니다. 이번 글에서는 직육면체의 부피와 겉넓이 그리고 사다리꼴 넓이 구하는 공식을 확인해보도록 하겠습니다.

아주쉬운 직육면체 부피와 겉넓이 공식 알아보기
직육면체란 무엇인가요?
먼저, 직육면체가 무엇인지 알아봅시다. 직육면체는 모든 면이 직사각형이며, 모든 모서리가 직각을 이루는 도형입니다. 우리가 흔히 알고 있는 물건들 중 많은 것들이 직육면체의 형태를 띠고 있습니다.
부피를 구하는 방법
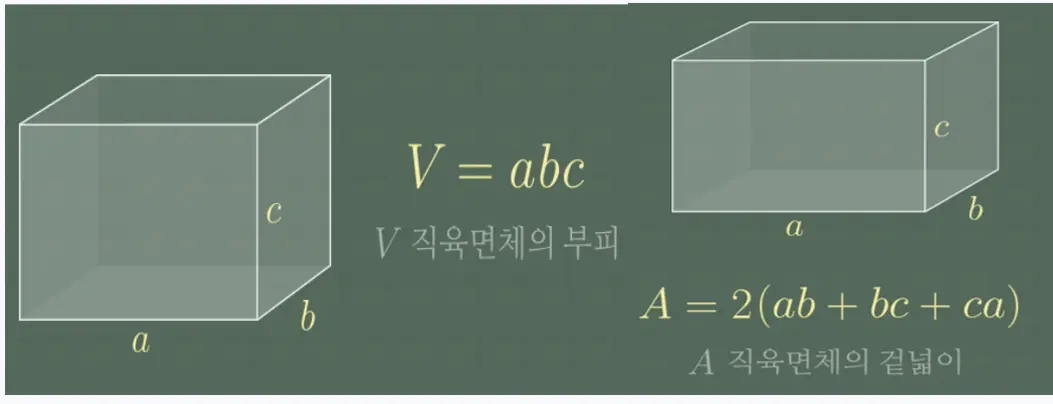
이제 직육면체의 부피를 구하는 방법에 대해 알아봅시다. 부피를 구하는 공식은 간단합니다. 바로 "길이 × 너비 × 높이"입니다. 이 때, 길이, 너비, 높이는 모두 직육면체의 서로 직교하는 세 변의 길이를 의미합니다.
부피를 구하는 단위는 일반적으로 입방 센티미터(cm³)나 입방 미터(m³) 등의 입방 단위를 사용합니다.
부피 예제
간단한 예를 들어보겠습니다. 만약 직육면체의 길이가 10cm, 너비가 5cm, 높이가 8cm라면, 부피는 간단히 곱셈을 통해 계산할 수 있습니다. 즉, 10cm × 5cm × 8cm = 400cm³가 됩니다. 따라서 이 직육면체의 부피는 400 세제곱 센티미터입니다.
겉넓이 공식
이제 직육면체의 겉넓이를 구하는 방법에 대해 알아봅시다. 겉넓이는 각 면의 넓이를 모두 합한 값입니다. 각 면의 넓이를 구하는 방법은 간단합니다. 예를 들어, "길이 × 너비"로 계산할 수 있습니다. 이 값을 모두 합하면 겉넓이가 됩니다.
겉넓이 예제
이전에 주어진 예제를 활용하여 직육면체의 겉넓이를 계산해보겠습니다.
"길이 × 너비"는 10cm × 5cm = 50cm², "길이 × 높이"는 10cm × 8cm = 80cm², "너비 × 높이"는 5cm × 8cm = 40cm²입니다. 이를 합하면, 겉넓이는 2 × 50cm² + 2 × 80cm² + 2 × 40cm² = 340cm²가 됩니다.
사다리꼴의 넓이 공식과 문제 예시
사다리꼴의 넓이 공식
우선 사다리꼴의 넓이를 구하는 공식을 살펴보겠습니다. 사다리꼴의 넓이를 구하는 공식은 다음과 같습니다.
넓이 = (밑변의 길이 + 윗변의 길이) × 높이 ÷ 2
이 공식은 사다리꼴의 밑변과 윗변의 길이, 그리고 높이를 알고 있을 때 사용됩니다. 간단히 밑변과 윗변의 길이를 더한 후 2로 나눈 다음, 그 결과에 높이를 곱해주면 사다리꼴의 넓이를 구할 수 있습니다.

문제 예시와 풀이 방법
이제 몇 가지 실제 문제 예시를 통해 사다리꼴의 넓이를 구하는 방법을 살펴보겠습니다.
문제 1
문제: 밑변의 길이가 6cm, 윗변의 길이가 4cm, 높이가 5cm인 사다리꼴의 넓이를 구하세요.
풀이:
- 주어진 값을 공식에 대입합니다.
- 밑변의 길이: b = 6cm
- 윗변의 길이: a = 4cm
- 높이: h = 5cm
- 공식에 값을 대입하여 계산합니다.
- 넓이 = (4cm + 6cm) × 5cm ÷ 2
- 넓이 = 10cm × 5cm ÷ 2
- 넓이 = 50cm² ÷ 2
- 넓이 = 25cm²
따라서, 주어진 사다리꼴의 넓이는 25cm²입니다.
문제 2
문제: 밑변의 길이가 9m, 윗변의 길이가 3m, 높이가 7m인 사다리꼴의 넓이를 구하세요.
풀이:
- 주어진 값을 공식에 대입합니다.
- 밑변의 길이: b = 9m
- 윗변의 길이: a = 3m
- 높이: h = 7m
- 공식에 값을 대입하여 계산합니다.
- 넓이 = (3m + 9m) × 7m ÷ 2
- 넓이 = 12m × 7m ÷ 2
- 넓이 = 84m² ÷ 2
- 넓이 = 42m²
따라서, 주어진 사다리꼴의 넓이는 42m²입니다.
마무리 하며
직육면체의 부피와 겉넓이 및 사다리꼴의 넓이 를 계산하는 공식을 알고 있다면, 다양한 문제를 해결하는 데 도움이 됩니다. 이러한 계산은 우리의 일상 생활과 다양한 분야에서 활용됩니다. 따라서 이러한 기본적인 수학적 개념을 숙지하는 것은 매우 중요합니다.
수학적 지식은 우리의 머리 속에 무한한 가능성을 열어줍니다. 직육면체의 부피와 겉넓이를 계산하는 과정을 통해 수학이 실생활에서 어떻게 활용되는지 알아보았습니다. 앞으로도 다양한 수학적 개념을 익혀서 현실 세계의 다양한 문제를 해결해 나가는 데 도움이 되기를 바랍니다.
✅함께 읽으면 좋은글
천재교육 교과서 PDF 다운로드 방법 I 고등 중등 한국사 수학 국어 과학 과목별
천재교육은 중학교부터 고등학교까지의 다양한 학년을 대상으로 통합사회, 한국사, 영어, 독서, 통합과학, 수학 교과서를 제공하고 있습니다. 이러한 교재들은 학생들의 학습을 돕기 위한 중요
newsphere.tistory.com
나이스 학부모 서비스의 모든 것 I 자녀 등록 생활기록부 조회 완벽 정리
나이스 학부모서비스는 현대 학부모들에게 꼭 필요한 유용한 정보와 서비스를 제공하고 있습니다. 이 서비스를 활용하면 자녀의 학교 생활을 더욱 효과적으로 관리할 수 있으며, 다양한 기능을
newsphere.tistory.com
교육급여 바우처 신청 자격 방법 대상 지급일 사용처 카드 잔액 누리집 가맹점 » Newsphere 한발 앞
교육비도 정부에서 지원되는 걸 알고 계셨습니까? 이제도는 저소득층을 위한 제도로 현재 초중고가 의무 교육이지만 이외에 학교생활에 필요한 교육비등을 정부에서 지원하는 제도가 있습니다
newsphere.co.kr






























'알뜰한생활정보' 카테고리의 다른 글
| GS25 틈새비김면 구입 후기 조리방법 리뷰 (제품 특징 및 할인 구매) (1) | 2024.04.29 |
|---|---|
| 주짓수 벨트 순서 승급 체계 그라우와 함께하는 수련 순서 알아보기 (0) | 2024.04.26 |
| 아주 쉽게 한방 정리 Netflix 넷플릭스 결제수단 변경 및 결제카드 등록 삭제 방법 (0) | 2024.03.30 |
| 10분 초간단 파김치 담그는법 노하우 만드는법 대공개 백종원 황금 레시피 소개 (2) | 2024.03.29 |
| 수정과 만드는법 초간단 황금레시피 I 수정과 재료 및 효능 꿀팁 안내 (0) | 2024.03.29 |




댓글